Kurven einer Partialsummierung komplexer Summanden, mit drei verschiedenen Parametern (-d,0,d)
Gottfried Helms 7'2006
Die
Punkte zeigen die Partialsummen einer bestimmten Reihenfunktion,
nämlich der Summanden der Euler-Summation für die
Eta-Funktion.
Die
Eta-funktion muß aufgrund des bekannten Zusammenhangs
zeta(s)*(1-2^-2)= eta(s) dieselben Nullstellen haben wie die
Zeta-funktion.
Die Riemannsche Hypothese ist, saß die Zeta-Funktion nie eine Nullstelle hat an zeta(t+d), wenn t = 1/2 + x i und d>0 .
Die Symmetrie der zeta-Funktion nutzend heißt das also
RH : zeta(t-d) = zeta(t+d) <> 0 für ale d mit 0<d<1/2
Die Folge ist für die eta-funktion ähnlich. Gäbe es ein gegenbeispiel hieße das
eta(t-d) = eta(t+d) = 0
oder
RH : norm(eta(t+d) - eta(t-d))<>0 für alle d mit 0<d<1/2
Es
gibt nun das Eulersche Summierungsferfahren, das eine Vorschrift
für die Approximation der eta-Funktion durch eine Reihe gibt:
Konvergenzpunnkt k(s)_oo
= 1 + a_1 + a_2 + ... -> eta(s) wobei die a_k
die Euler-Summanden sind.
Die a_k haben die Form
(hier nur ungefähr angegeben) : b_k / 2^k, sodaß die
Hoffnung besteht, daß das exponentielle Wachstum des Nenners die
Summanden in ihrer Größe begrenzt.
Für eta(t-d) , eta(t) und eta(t+d) laufen die Summanden weitgehen genau parallel:
b(t-d)_k , b(t)_k, b(t+d)_k ~ parallel.
Kann
nachgewiesen werden, daß die Abstandsnorm von (b(t-d)_k -
b(t+d)_k) für k-> inf sowie deren Partialsummen s(t-d)_k,
s(t+d)_k nicht verschwindet, gibt es keine Nullstellen mit d>0.
und die RH ist bewiesen.
Hier sind Kurven, die
mit einem positiven (hellblau, +d), einem Null (rot, 0) und einem
negativen Parameter (grün,-d) erstellt werden., die
gekrümmten Kurven sind einfache Interpolationen der Punkte
(Excel).
Die geraden Linien verbinden zusammengehörige Teilterme der Summierung mit Positiv- Null und Negativparameter.
Ausgangspunkt der Kurven ist (1, 0 i); Konvergenzpunkte sind die Häufungspunkte an den anderen Enden.
Das ganze Bild erscheint als Projektion eines 3-D Objekts, das möglicherweise neben
der Rotation in 3 D zusätzlich eine Verwindung haben könnte.
Es
sieht so aus, als ob die Teilterme der Null-parameter Zentrum einer
fast perfekten Symmetrie der Punkte mit positiven und negativem
Parameter sind, wenn man
die Rotation in 3 D berücksichtigt (Abweichungen könnten auf Rundungsfehler zurückzuführen sein)
.Dies
sind die Partialsummen der Eulersummierung für die Eta-Funktion mit t=(1/2, 14.3... i ) d.h. an der ersten Nullstelle
der Zeta/Etafunktion, wobei mit d=0.1 die drei
Partialsummenkurven blau für eta(t-d),rot eta(t), grün
eta(t+d) entstehen
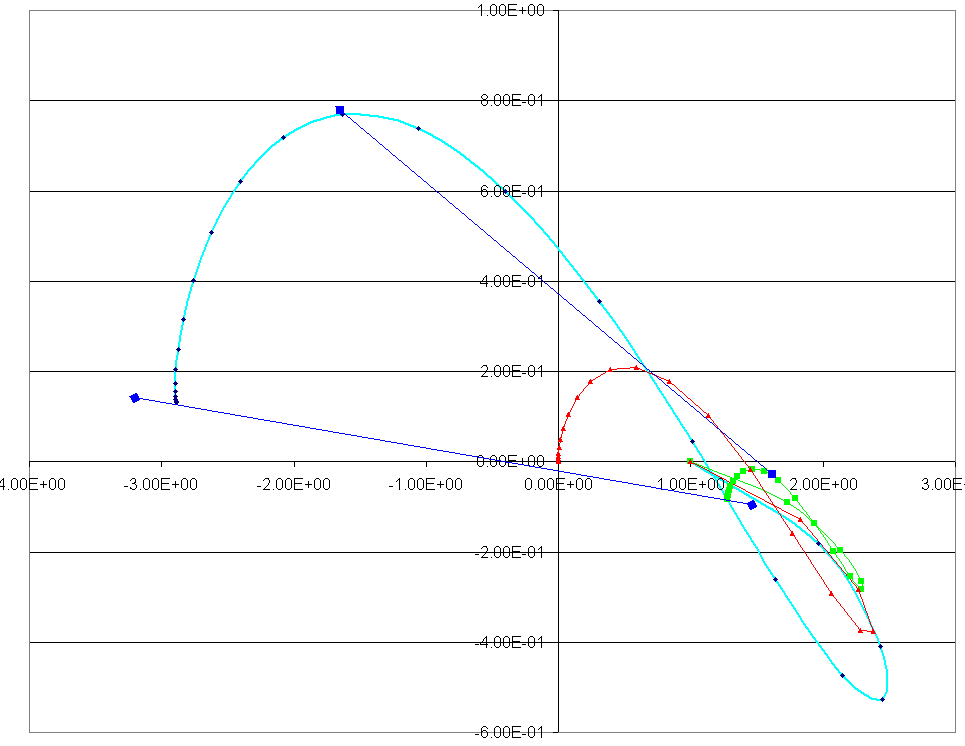
Man
sieht, wie die rote Kurve der Partialsummen für eta(t) ausgehend
von (1,0 i) gegen den Nullpunkt (0,0 i) konvergiert und somit die
erste Nullstelle der eta/zeta-Funktion approximiert. Die Konvergenten
für eta(t+d), eta(t-d) weichen hier offensichtlich und deutlich
sichtbar von eta(t)/zeta(t) = 0 ab.
Dies
sind die Partialsummen der Eulersummierung für die Eta-Funktion an
einer beliebiegen anderen Stelle t = (1/2,18), s(t-d), s(t),s(t+d)

Die
grünen und blauen Devianzen von den s(t)-summanden sind fast genau
zentralsymmetrisch, und als 2-D-Projektion eines 3-D-Objektes
betrachtet verläuft die grüne Kurve strikt rechts und die
blue Kurve strikt linksseitig zur Zentralkurve. D.h. wir haben nicht
nur einen fast monoton wachsenden Abstand zur Zentralkurve, sodern auch
eine eindeutige Separierung. Es ist anzunehmen, daß die
Konvergenten der drei verschiedenen Kurven stets fast linear
abhängig mit einem Abstand symmetrisch zur zentralkurve sind.
Die
Abstände der Konvergenzpunkte k-, k und k+ sind hier weiter
interessant, sowie die Frage, wieweit die drei Punkte auf einer Geraden
liegen.
Hierzu
berechne ich einfach die Determinante des Dreiecks (k-,k,k+),
praktisch die Determinante der durch 0, k-' und k+' aufgespannten
Fläche, wenn die drei Punkte zu k=(0,0) verschoben sind. Grafik
für verschiedene imaginäre Werte von t mit konstantem d siehe
weiter unten.
| x |
y |
x |
y |
x |
y |
| 1.0000 |
0.0000 |
1.0000 |
0.0000 |
1.0000 |
0.0000 |
| 1.1144 |
0.0014 |
1.1464 |
0.0013 |
1.1758 |
0.0012 |
| 1.0579 |
-0.1427 |
1.1117 |
-0.1243 |
1.1616 |
-0.1082 |
| 0.9379 |
-0.3594 |
1.0123 |
-0.3132 |
1.0810 |
-0.2728 |
| 0.7566 |
-0.5489 |
0.8592 |
-0.4798 |
0.9523 |
-0.4192 |
| 0.5205 |
-0.6473 |
0.6610 |
-0.5703 |
0.7861 |
-0.5019 |
| 0.2454 |
-0.6336 |
0.4320 |
-0.5673 |
0.5954 |
-0.5066 |
| -0.0542 |
-0.5181 |
0.1849 |
-0.4799 |
0.3914 |
-0.4411 |
| -0.3688 |
-0.3301 |
-0.0722 |
-0.3325 |
0.1811 |
-0.3259 |
| -0.6925 |
-0.1071 |
-0.3341 |
-0.1557 |
-0.0312 |
-0.1860 |
| -1.0180 |
0.1146 |
-0.5952 |
0.0211 |
-0.2409 |
-0.0452 |
| -1.3349 |
0.3065 |
-0.8477 |
0.1751 |
-0.4422 |
0.0782 |
| -1.6305 |
0.4518 |
-1.0820 |
0.2928 |
-0.6281 |
0.1735 |
| -1.8927 |
0.5460 |
-1.2892 |
0.3705 |
-0.7920 |
0.2373 |
| -2.1128 |
0.5942 |
-1.4630 |
0.4119 |
-0.9293 |
0.2726 |
| -2.2874 |
0.6070 |
-1.6010 |
0.4253 |
-1.0384 |
0.2856 |
| -2.4183 |
0.5968 |
-1.7047 |
0.4200 |
-1.1205 |
0.2837 |
| -2.5110 |
0.5746 |
-1.7785 |
0.4048 |
-1.1792 |
0.2734 |
| -2.5732 |
0.5487 |
-1.8283 |
0.3860 |
-1.2191 |
0.2599 |
| -2.6125 |
0.5241 |
-1.8600 |
0.3679 |
-1.2447 |
0.2466 |
| -2.6359 |
0.5035 |
-1.8791 |
0.3524 |
-1.2603 |
0.2350 |
| -2.6488 |
0.4876 |
-1.8899 |
0.3403 |
-1.2692 |
0.2258 |
| -2.6554 |
0.4761 |
-1.8956 |
0.3315 |
-1.2740 |
0.2191 |
| -2.6584 |
0.4683 |
-1.8982 |
0.3254 |
-1.2763 |
0.2144 |
| -2.6595 |
0.4631 |
-1.8993 |
0.3214 |
-1.2773 |
0.2113 |
| -2.6596 |
0.4599 |
-1.8996 |
0.3189 |
-1.2777 |
0.2093 |
| -2.6594 |
0.4579 |
-1.8995 |
0.3173 |
-1.2777 |
0.2081 |
| -2.6591 |
0.4568 |
-1.8993 |
0.3164 |
-1.2776 |
0.2073 |
| -2.6588 |
0.4561 |
-1.8991 |
0.3159 |
-1.2774 |
0.2069 |
| -2.6586 |
0.4558 |
-1.8990 |
0.3156 |
-1.2773 |
0.2067 |
| -2.6584 |
0.4556 |
-1.8988 |
0.3154 |
-1.2773 |
0.2065 |
| -2.6583 |
0.4555 |
-1.8988 |
0.3153 |
-1.2772 |
0.2065 |
| -2.6583 |
0.4554 |
-1.8987 |
0.3153 |
-1.2772 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8987 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8987 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8987 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
| -2.6582 |
0.4554 |
-1.8986 |
0.3153 |
-1.2771 |
0.2064 |
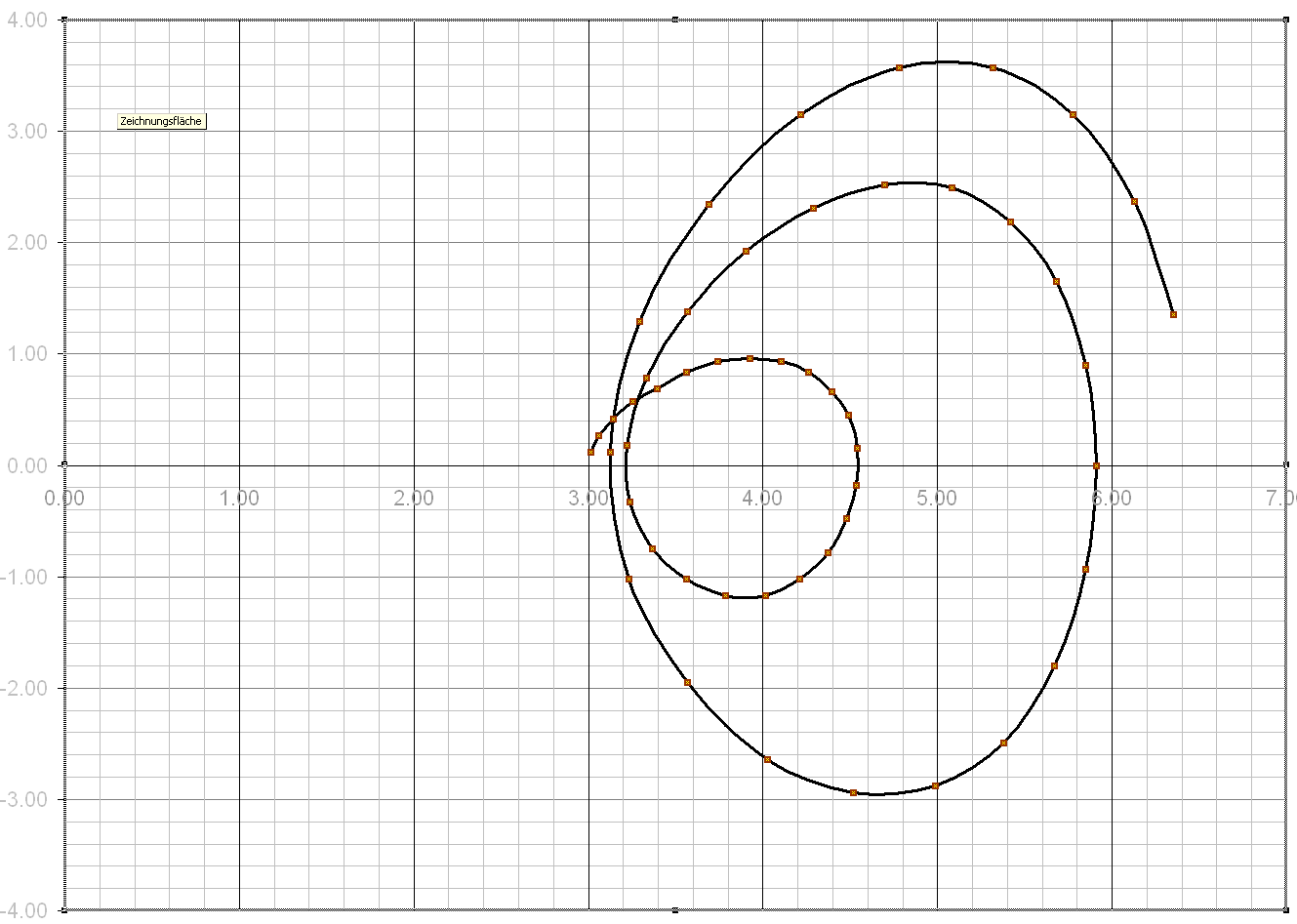
In der folgenden Kurve wird mit einem
festen d von 0.2 der imaginäre Anteil von t=(1/2,x i)
verändert. x wandert hier von 14.134 (1. Zeta Nullstelle)
über
21... (zweite Nullstelle) bis 21,....+14,... der Anfang
der Spirale ist hier für die rote Zentralkurve (0,0).; diese
Nullstelle wird bei 1 1/2 Umläufen wiedrum erreicht und die Kurve
endet bei etwa (-0,5,4 i)
Man sieht, daß die Kurven mit t+d bzw t-d strikt auf gegensätzlichen Seiten der Zentralkurve verlaufen.
Um
eine Nullstelle der eta-Kurve/Zeta-Kurve mit einem positiven d zu
haben, müßten diese Abstände bei einem gewissen x gegen
0 gehen. (Man hätte dann außerdem
eine
dreifach-Nullstelle der Zeta-Funktion, da alle drei Kurven (und evtl
alle mit dazwischenliegenden d ebenfalls) Null wären.

Norm
und determinante der Abstände eta(t-d) eta(t+d) und Determinante
(eta(t-d)-eta(t), eta(t+d)-eta(t) ), mit Maßstab für x-achse
(norm) *100 skaliert, und der Maßstab für die y-Achse
(Determinante) mit 10000 skaliert.
Wenn
entweder für die Größe der Norm eine untere oder
für die Determinante eine obere absolute oder funktionale Grenze
angegeben werden kann (was hier so aussieht) gibt es keine Nullstellen
der eta/zeta-Funktion für eta(t+d),zeta(t+d) mit d>0
Gottfried Helms



