MatMate

Matrizen-Taschenrechner
unter Windows 98

Version: Testversion 0.0207
Jul 2002

Gottfried Helms
Universität Kassel

email: helms@uni-kassel.de

MatMate Einfuehrung

MatMate ist für Matrizenrechnen das, was für normales Rechnen ein einfacher "Taschenrechner" ist: ein einfach zu bedienendes Werkzeug auch für nebenbei zu bewältigende Zwischenrechnungen. Auf eine Simulation der Knöpfcheneingabe wie bei Taschenrechnern üblich wurde dennoch verzichtet; stattdessen hat man ein Eingabefeld für eine Zahl oder Formel - genauergenommen sogar eine ganze Textdatei.
Der Befehl x=7 erzeugt ein Anzeigefeld namens X und zeigt dort die Zahl 7 an. Der Befehl a=4*(3+x)^2 erzeugt ein Anzeigefeld namens A und zeigt dort das Ergebnis der Formel an, unter Einrechnung des X, das soeben vorher berechnet wurde.

Sie tippen die Befehle so wie sie hier stehen, wie in einer Textverarbeitung. Dabei haben Sie alle Möglichkeiten der Tippfehlerkorrektur, Übernahme von Zeilen aus Ihrer Textverarbeitung via Clipboard etc. Um den Befehl auszuführen lassen Sie die Cursormarke auf der Zeile und drücken das Knöpfchen Run!

Also

A= m_mksp(1,2,3,4)
b= a * a'

Markieren Sie beide Zeilen schwarz, dann können sie mit Einem RUN!-Befehl ausgeführt werden.

Statt des Knopfes RUN! können Sie einfach die Tastenkombination ALT-R drücken - dann brauchen Sie nicht ständig zwischen Maus und Tastatur zu wechseln.

MatMate ist noch nicht vollständig ausprogrammiert; insbesondere bekommen Sie noch keine Fehleranalyse für Tippfehler: was nicht geht, wird meist einfach übergangen. Da es aber bereits jetzt nützlich für einfache Rechnungen wie auch für tiefere Analyse von Matrizenrechnungen ist, möchte ich es jetzt als Beta-/Testversion veröffentlichen.

Rechnen

Es sind alle Standardrechenarten und einige spezielle Funktionen (meist für Untersuchung der Korrelationsanalyse) implementiert. Darunter sind die 4 Grundrechenarten, Potenzierung, Exponential und trigonometrische Funktionen, sowie viele Matrizenfunktionen, bei denen sich auch ein großer Teil mit dem Extrahieren von Teilmatrizen und Zusammensetzen von Matrizen beschäftigt.

Die Ergebnisse werden in dem 2. Fenster, dem MatMate-"Matrizen-Regal" angezeigt: alle Matrizen haben ein eigenes kleines Windows-Fenster, und alle skalaren Ergebnisse haben eine Zeile in einem gemeinsamen Ausgabefenster.

Die Formelsprache / die Syntax

1 Befehl pro Zeile

Grundprinzip ist: eine Zeile - ein Berechnungs-Befehl: Cursor setzen - Formel eintippen - Run! - Ausrechnen.

Am Ende jeder Zeile kann zusätzlich ein beliebiger Kommentar stehen, z.B. weil Sie lange Befehlsfolgen abspeichern und beschreiben wollten. Trennen Sie einen Kommentar durch einen Doppelschrägstrich //, also zwei aufeinanderfolgende / von der Formel ab.

Eine Berechnung ohne Kommentar

a = m_mksp(1,2,3,4)

mit Kommentar

a = m_mksp(1,2,3,4) // eine 1-spaltige Matrix
// mit 4 Einträgen anlegen

Eine Zeile kann auch fortgesetzt werden; am Ende muß dann ein einzelnes Unterstreichungszeichen stehen (wie in Visual Basic)

a = { {1,2}, _
{3,4} _
} // eine 2x2 Matrix anlegen

Der Cursor muß in eine der auszuführenden Zeile gesetzt werden. Die Zeilengruppe braucht nicht markiert zu werden.

mehrere Befehle

Es können auch mehrere Befehle zusammen ausgeführt werden. Mann muß dann die Markierung auf die gewünschten Zeilen erweitern.

a = m_mksp(1,2,3,4)
b = a * m_transp( a )

Die Markierung überstreicht beide Zeilen; der Cursor kann irgendwo stehen. Run! drücken. Beide Zeilen werden zusammen ausgeführt.

Ist eine Markierung vorhanden, werden alle Zeilen, die von ihr berührt werden inclusive evtl vorhandener vorlaufender und nachlaufender Fortsetzungszeilen ausgeführt. Ein komplexes Beispiel:

a = m_mk (2,2, _
1,2, _
3,4) // eine 2x2 Matrix anlegen
b = m_mk (2,2, _
1,3, _
2,4) // die Transponierte anlegen
c = a * b - _
b * a // Matrixmultiplikationen

Alle 3 Befehle, die hier von der Markierung berührt werden, werden komplett gelesen und ausgeführt. Der Cursor braucht in diesem Fall NICHT in einem der Befehle zu stehen. Die Markierung wird nach Ausführung nicht entfernt; Befehle können deshalb iteriert werden, indem man einfach Run! oder die Alt-R-Taste mehrmals drückt.

Ist KEINE Markierung vorhanden, wird die Zeile ausgeführt, in der sich der blinkende Cursor befindet.

einfaches Ändern der Daten einer Matrix

Neben der einfachen Berechnungsweise für Matrizen ist auch die direkte Werteingabe ein praktisches Feature, mit denen Veränderungen im Input einer Formel schnell ausprobiert werden können. (Allerdings erscheinen diese manuellen Änderungen derzeit noch nicht im Journal)

Arbeiten mit Daten aus der Literatur

Dadurch, daß die Bedienung des Matrizenrechners über eine Skriptsprache funktioniert, können Sie Matrizen, die Sie aus der Literatur übernommen haben, als Text-/Skript-Eingabe speichern, und Ihre Untersuchungen später mit demselben Datenmaterial reproduzieren oder abwandeln.

Journal

Alle ausgeführten Befehle werden in einem Journal protokolliert. Diese Datei wird anschließend automatisch gespeichert. Durch die Journal-Funktion können Sie alle Berechnungsschritte reproduzieren, eventuelle Denkfehler untersuchen und verbessern. Insbesondere bei Iterationen ist das Journal vorteilhaft: alle Iterationsschritte sind sequentiell hintereinander aufgezeichnet und können später en bloc wiederholt werden.

Interaktion mit anderen Programmen unter Windows

Es gibt 3 Schnittstellen: Da Sie Befehle/Formeln tippen, haben Sie die Möglichkeit Ihre Arbeiten und Analyseschritte in normalen Textdateien zu spreichern. Die berechneten Matrizen können Sie außerdem in Dateien an andere statistische oder mathematische Programme übergeben oder sie in denselben Formaten von dort aus einlesen. Die dritte Möglichkeit ist die Windows-Zwischenablage, über die Sie Matrizendaten z.B. direkt an Excel oder Winword übergeben können.

(Aktuelles)

· COMP c = <formel>

In der aktuellsten Version kann der Befehlsteil COMP überall entfallen. Die Grafiken in diesem Heft zeigen noch den Stand der vorigen Version. Die dort dargestellte Syntax funktioniert aber immer noch.

Formel ausrechen:

Neu:

A = {1,2,3} * {1,2,3} '

Alt:

COMP A = {1,2,3} * {1,2,3} '

Ziele / Begrenzungen

Tool zur Matrizenrechnung

Das Hauptziel dieses Programms ist die Unterstützung des Selbststudiums der Hintergründe und Vorgänge bei der Matrizenrechnung. Man kann viele Rechenprozesse aus der Literatur nachvollziehen und transparent machen.

Es ist bisher NICHT intendiert, eine vollständige Programmiersprache zu entwickeln. Es ist ebenfalls bisher nicht intendiert, ein symbolisches Algebrasystem zu implementieren. Hierzu gibt es bereits diverse professionelle und semiprofessionelle Angebote, und sogar Freeware-Versionen. MatMate will dazu nicht in Konkurrenz gehen.

Eventuell wird es in einer nächsten Version eine Makro-Sprache geben, sofern sie ohne Änderung des momentan vorhandenen Einfachst-Konzeptes integriert werden kann.

Anzeigen der Ergebnisse/Ausgabeprotokoll

Der Schwerpunkt liegt -neben der Verfügbarkeit eines billigen Matrizenrechners auf Leistungskurs- und College-Niveau - auf der Sichtbarmachung der Rechenvorgänge. Durch die Präsenz der Matrizenanzeige wird die Matrixalgebra besonders transparent. Die Matrixergebnisse kann man via Clipboard in konventionelle Textverarbeitungsprogramme übernehmen.

Eventuell wird es in Zukunft ein laufendes Ausgaben-Fenster geben, in das Ergebnisse zusammen mit den Formeln/befehlen dokumentiert werden, sodaß matrizenanalytische/statistische Artikel unter Einbeziehung der Operationen und Ergebnisse direkter geschrieben werden können

Betaversion

Es handelt sich hier noch um eine Beta-Version, für die noch Listen an zu verbessernden Optionen bestehen.

Insbesondere gibt es noch keine besondere Fehleranalyse; Fehler in der Syntax oder während einer Berechnung führen meist einfach zum Überspringen des betreffenden Befehls, und evtl der Folgebefehle. Programmabstürze sind immerhin in der aktuellen Testphase noch nicht aufgetreten - d.h. Arbeitsergebnisse und Skripte sind noch nicht verloren gegangen.

Auch sind einige mathematische Verfahren noch nicht vollständig stabilisiert; hier sind meist einfach die von Borland-Delphi gelieferten Methoden übernommen. Meist wird hierbei mit Extended-Präzision gearbeitet, es gibt einige Double-Precision-Module. D.h. Genauigkeit bei numerischen Operationen Zahlen liegt bei ca 15 Dezimalstellen.

Die Größe von Arrays/Matrizen wird von 32-bit Integer-Variablen verwaltet; dh. sie dürften praktisch nur durch den bei Ihnen vorhandenen Hauptspeicher begrenzt sein.

· Keine Garantie für Datenverluste unmittelbar oder mittelbar.

einfache Beispiele

skalarer Rechner

Die Grundrechenarten sowie logarithmische und trigonometrische Funktionen sind implementiert. In den Formeln können Klammern beliebig tief verschachtelt werden. Man kann auf bereits berechnete Ergebnisse zurückgreifen, da jedes Ergebnis einer (skalaren) Variablen (also einem benanntem Anzeigefeld) zugewiesen wird, auf das Sie sich in einer nächsten Formel beziehen können. "Skalar" ist hier die Bezeichnung für einen einzelnen Wert, in Abgrenzung (dieser gewöhnlichen) Rechnung mit einzelnen Zahlen von der Rechnung mit Vektoren, Matrizen und Arrays.

Anzeigen skalarer Ergebnisse

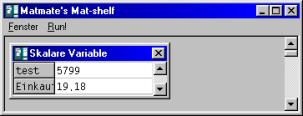
Wenn Sie einen einzelnen Wert so wie auf dem Taschenrechner berechnen wollen, tippen Sie einfach die Formel (Verwenden Sie den Punkt als Dezimal-Trennzeichen):

EinkaufSumme = 1.12 + 4.50 + 3.38 + 2.50 + 7.68

Im Anzeigefeld "skalare Variable" wird die Einkaufssumme angezeigt.

oder

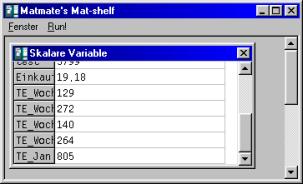
// TE_Woche1 : Telefoneinheiten in der Woche Nr...
TE_Woche1= 12+23+45+16+23+8+2
TE_Woche2= 14+13+ 5+ 2+11 + _
+23 + 78 +126
TE_Woche3 = 11+23+45+1+1+3+2+6+8+8+9+11+12
TE_Woche4 = 1+5+12+45+67+2+42+64+26

// TE_Jan: Telefoneinheiten für Monat Januar
TE_Jan = TE_Woche1 + TE_Woche2+ _
TE_Woche3+TE_woche4

Im Anzeigefeld "skalare Werte" werden die Wochensummen und die Summe für Januar angezeigt.

komplexere Formeln

Formeln können Klammern enthalten und beliebig komplex werden. Neben den arithmetischen Rechenarten können auch logische Vergleiche und eine einfache Form des bedingten Rechnens verwendet werden.

x= (a^3 + 3*a*5*(a + 5) + 5^3)^(1/3)
phi2 = 1- cos(phi)^2
root = sqrt(a-b) if (a>=b) else sqrt(b-a)
umf = 2*radius*#pi^2

Sie können in den Formeln #pi und #e, sowie #false und #true als Konstanten angeben.

Beispiel mit Iterationen

Z.B. wollen Sie nachvollziehen, wie mit dem Newton-Verfahren die Wurzel aus 14 berechnet wird. Das übliche Ergebnis berechnen Sie einfach mit der gewöhnlichen Taschenrechnerfunktion.

Y = sqrt(14)

Es wird eine Anzeigezeile für das Ergebnis erzeugt, und dies erhält den Namen Y. Sie können beliebige Namen bis zur Länge von 16 Buchstaben wählen:

standard_Y = sqrt(14)

Nun programmieren Sie das Newton-Verfahren. Man nimmt einen Probewert, setzt ihn in die Newton'sche Formel ein, berechnet einen neuen Wert, der wegen der Konstruktion der Formel besser ist als der erste und nimmt diesen dann als neuen Probewert. Das macht man solange, bis der Wert sich nicht mehr (nennenswert) ändert.

wert=1 // einen Anfangswert einstellen

Fürhren Sie den obenstehenden Befehl aus. wert wird angezeigt. Tippen Sie dann die beiden folgenden Befehle und führen Sie sie zusammen aus (Markierung auf beide Zeilen erweitern und Alt-R drücken):

altwert = wert
wert = (14 / altwert + altwert) / 2

Die Anzeigezeile für altwert wird eingestellt, und für wert wird gleich die neue Version ausgerechnet. Wiederholen (iterieren) Sie jetzt diese Befehlsfolge, bis sich wert nicht mehr wesentlich ändert. Er sollte dann mit standard_y übereinstimmen. Die verbliebene Ungenauigkeit können Sie sich anzeigen lassen, indem Sie wert von standard_y abziehen:

chk = wert - standard_y

Durch die Anzahl der Iterationen können Sie die Wurzel aus 14 beliebig genau bestimmen. Die Grenzen der maximalen Genauigkeit sind hier die des Betriebssystems, dessen DOUBLE-Genauigkeit verwendet wird, z.B. PC bis ca 16 Dezimalstellen.

Matrizenrechner

MatMates Hauptanliegen ist die Unterstützung bei der Matrizenrechnung.

Über die Grundrechenarten hinaus sind auch arithmetische Funktionen für Matrizen implementiert, die nicht nur auf Einzelelementebene, sondern mit der Matrix als Ganzes operieren, wo dies durch die Definition der Funktion Sinn macht.

Nachdem die Matrix-Multiplikation die Matrix als Ganzes behandelt, wird dies auch in allen Funktionen so gehandhabt, die aus der Multiplikation abgeleitet sind, z.B. die exponential- und trigonometrischen Funktionen, deren Definition in einer Summe aus Produkten bzw. Quotienten besteht.

Soll eine solche Funktion sich stattdessen auf die einzelnen Elemente beziehen (z.B. der Logarithmus jedes einzelnen Elements) muß die Matrix temporär als Array verwendet werden; dies wird durch den nachgestellten Array-Operator # eingestellt (Beispiele siehe unten).

Anzeigen von Matrizenergebnissen

Alle berechneten Ergebnisse, die in einer Matrix abgespeichert werden, werden sofort angezeigt. Die Form ist z.Zt. ein einfaches dezimales-Fixed-Format; dieses kann über den SET-Befehl verändert werden.

Verbergen/Löschen von Matrizen

Haben einige Matrizen nur temporäre Funktion, deren Anzeige nicht interessiert, können sie durch den HIDE- bzw DELETE Befehl scriptgesteuert versteckt bzw. gelöscht werden, wodurch sich das MatMate - MatShelf lichten läßt. Der Hide-Befehl wird auch implizit durchgeführt, wenn Sie das Fenster einer angezeigten Matrix schließen.

Ist eine Matrix mit DELETE gelöscht, kann sie nicht mehr als Quelle in einer Formel verwendet werden, sondern muß erst wieder durch eine Zuweisung erzeugt werden. Sie können aber eine Matrix ausblenden ohne sie zu löschen, wenn Sie das Fenster minimieren oder die HIDE-Funktion verwenden. Durch DISPLAY wird sie wieder angezeigt.

Interaktion mit anderen Programmen

Clipboard

Die Anzeige einer Matrix kann ins Clipboard übernommen werden; dort liegt dann eine Tabulator-getrennte Form vor, die z.B. von Excel oder Winword als Tabellenformat erkannt wird. Die von MatMate verwendeten Dezimalpunkte werden dabei in die für diese Programme gültige Schreibweise mit Kommas umgewandelt. (Menü MATRIX/KOPIEREN…)

Dateien

Matrizen können aus Dateien gelesen und geschrieben werden. Dies geht z.zt. im CSV-Format ("comma separated values"), im Binärformat und Hexadezimal-Textformat, das SPSS^® verwendet (Binär: eine double-Speicherstelle pro Element, am Ende einer Zeile ein zusätzliches CrLF, pro Matrixzeile eine Dateizeile) sowie die Ladungsmatrizen meines interaktiven Faktoranalyse-Programms Inside-[R] (z.Zt. nur lesen).

komplexere Formeln

Genau wie skalare Variable können Matrizen in komplexen Formeln verwendet werden. Die Rückgabewerte von Matrixfunktionen sind in der Regel selbst wieder Matrizen, so daß auch alle Matrix-Funktionen beliebig verschachtelt werden können.

a = {{4,1},{1,5}}
b = m_inv(a)*m_inv( {{5,1},{1,5}}
lad= m_rot(m_cholesky(m_covar2corr(a)),"PCA")

Zur Unterstützung der Schreibarbeit gibt es einige Vereinfachungen wie z.B. für die Transposition die postfix-Notation mit dem Apostroph

b = a * m_transp(a) // oder 2. Schreibweise:
b = a * a'

oder den Verkettungsoperator, der Matrizen vertikal aneinanderkettet.

b = a || m_mksp( 1,3 ) || m_null(m_like(a))

Einfaches Beispiel mit Iterationen

Bei Matrizenproblemen muß oft mit Iterationen gearbeitet werden; bspw. kann man auch die Wurzel einer Matrix mit dem Newton-Algorithmus finden, wenn man die Division einer Matrix durch eine andere definiert. In MatMate wird der Divisionsoperator so interpretiert, daß der Divisor durch seine Inverse ersetzt wird, und der Dividend hiermit multipliziert wird. (Dies funktioniert u.U. auch mit nicht-quadratischen Matrizen, wenn eine Pseudoinverse gebildet werden kann). Deshalb kann die Newton-Iteration genau analog zu dem skalaren Beispiel durchgeführt werden:

Erzeugen einer Matrix, aus der die Wurzel gezogen werden soll; das ist z.B. grundsätzlich möglich bei einer Korrelations-Matrix:

// eine 2x2-Korrelationsmatrix erzeugen
CORR = m_mk(2,2, 1,0.8, 0.8,1)

Nun muß ein Anfangswert für WERT eingestellt werden:

WERT = m_einh(2) // eine 2x2-Einheitsmatrix

Führen Sie den obenstehenden Befehl aus. WERT wird angezeigt.

Tippen Sie dann die beiden folgenden Befehle und führen Sie sie zusammen aus (Markierung auf beide Zeilen erweitern und Alt-R drücken):

TMP = WERT
WERT = (CORR / TMP + TMP) / 2

Die Matrixdivision und -addition, sowie die skalare Division (aller Elemente durch 2) wird durchgeführt, und ein neuer Wert für WERT berechnet. Wenn Sie die beiden Zeilen mehrfach iterieren, erhalten Sie in WERT schließlich eine Matrix, für die gilt:

CORR = WERT * WERT // nicht transponiert!

und die (symmetrische) Wurzel von CORR darstellt.

(Für die Faktorenanalyse mag interessant sein, daß diese eine Ladungsmatrix darstellt, die für Rotationen zur PCA-Position, Quartimax- oder einer anderen Position verwendet werden kann - und zwar ebensogut wie eine durch die Cholesky-Zerlegung gewonnene Ladungsmatrix. Im Gegensatz zu letzterer Zerlegungsart sind bei dem Newton-verfahren aber keine elementaren Wurzeloperationen notwendig.)

gewöhnliche Probleme

· Einlesen von Matrizen aus Dateien funktioniert nicht

Der Befehl

c = M_readCSV("meineCSVdatei.txt")

funktioniert nicht richtig; c wird nicht angezeigt.

Mögliche Ursache(n):

Die Beispieldaten liegen im Unterverzeichnis "BEISPIELE" zum Programmverzeichnis. Durch einen Datei-Öffnen-Befehl wurde das aktuelle Verzeichnis geändert. MatMate findet dann diese Datei nicht. Geben Sie ggfs. in Ihren Skripten immer den vollständigen Verzeichnispfad an.

· Wie oben, aber c hat falsche Daten

Mögliche Ursache(n):

Das Format der Daten wurde nicht mit MatMate angelegt und kann nicht gelesen werden. Überprüfen Sie die Trennersymbole zwischen den Feldern und die Dezimalzeichen. Fehlen führende Nullen bei Dezimalzahlen ( z.B. .1234 kann nicht gelesen werden)?
Passen Sie die Optionen für CSV-Daten-einlesen ggfls an.

· Eine Matrix wird nicht angezeigt:

Der Befehl

c = A + B + sqrt(E)

funktioniert nicht richtig; c wird nicht angezeigt.

Mögliche Ursache (n):

Eine der Quellmatrizen existiert nicht. E ist nicht quadratisch. A, B und E haben nicht dieselbe Dimensionen. Prüfen Sie diese Möglichkeiten

Komplette Syntax

Allg. Programmbefehle

Außer Formeln gibt es auch einige Befehle, die MatMate ausführen kann:

· Programmparameter setzen / anzeigen

Setzt Optionen für das Kopieren in die Zwischenablage. (Anzeige der aktuell verfügbaren Optionen und deren Einstellungen durch SHOW)

set ccSchema="office" ccFeldweite=8
show

· Matrix in Datei ausgeben

gibt die Matrix mFctr in der PCA-rotierten Version in die Betriebssystem-Datei "c:\stat\mmpca.txt" aus. Das Ausgabeformat kann z.B. von SPSS^® gelesen werden (Format pbinhex)

Matwrite hex("c:\stat\MMPCA.txt") = m_rot(mFctr,"PCA")

MatWrite <typ>(<matname> [,<option>])=<formel oder variablenname>

· Kommagetrenntes Format.
Option:1 Zeichen Feldtrenner, 2.Zeichen Dezimalpunkt

MatWrite CSV("mymat.txt",feldweite,dezstellen,";,")=<expr>

· Hexadezimales Textformat.
Interne Darstellung (Double) in 2 ASCII-Hexziffern(0..9,A-F) pro byte.
16 Zeichen pro Feld,
Zeilenvorschub am Ende
Kann von SPSS^® pbinhex gelesen werden

MatWrite HEX("mymat.hex")=<expr>

· Binäres Internformat.
Interne Darstellung (Double)
8 Byte pro Feld,
Zeilenvorschub am Ende
Kann von SPSS^® binär gelesen werden

MatWrite BIN("mymat.bin")=<expr>

· Formel berechnen

myCorr = m_covar2corr(x*x'/N)
myFactors=m_cholesky(myCorr)

· Matrizen anzeigen/ausblenden

hide a,myCorr
display myFactors

· Programm beenden

quit

Formelzeile / Fortsetzungssymbol

Zeilen können beliebig lang sein (32 KB). Komplexe Befehle können aber auf mehrere Zeilen umgebrochen werden - dann muß an jeder fortgesetzten Zeile ein Fortsetzungszeichen (Leerzeichen-Unterstrich) folgen

Matwrite _ // ein Kommentar darf noch folgen
hex("c:\statistik\MMPCA.txt")= _
m_rot(myFactors,"PCA")

Kommentarsymbol

Dem Programmmcode können Kommentare hinzugefügt werden. Hierzu gibt es ggw. zwei Symbole: das Semikolon, der Doppelschrägstrich. Eine Zeile, die mit Semikolon beginnt, wird nicht bearbeitet. Da ds Semikolon aber ggfls für Listenaufzählungen verwendet werden wird, muß ein anderes Symbol für einen Kommentar, der die Zeile abschließt, verwendet werden: der Doppelschrägstrich

; dieser Kommentar ist mit einem Semikolon eingeleitet
a=b+c // so kann ein Kommentar am zeilenende angefügt
// werden

Namen

Namen in MatMate können bis zu 64 Zeichen lang sein, und nach einem Buchstaben auch Zahlen und Unterstriche enthalten. Groß-und Kleinschreibung wird nicht unterschieden; sie können also Ihre Matrizen- und Variablennamen schönschreiben. Namen können sogar mit Funktionsaufrufen gleichlauten.

Dies wird aber nicht empfohlen, da eventuell in einer späteren Version mit differenzierteren Variablenzugriffen evtl das gegenwärtig einfache Unterscheidungsmerkmal "Name (" = Funktion aber "Name " = Variablenname nicht mehr beibehalten werden kann.

Parametertypen und ~konventionen

Die Typprüfung bei Funktionsaufrufen ist noch nicht vollständig; d.h. eine Funktion versucht womöglich eine Operation durchzuführen, die auf den aktuellen Parameter nicht anwendbar ist und bricht die laufende Operation (-sgruppe) mit einer Programmfehlermeldung ab (das Programm selbst wird dabei nicht abgebrochen).

Die Hilfefunktion, die Sie nach drücken der rechten Maustaste erhalten, gibt Kurzhinweise mit Parametertypen.

a=abs(G) // die Absolut-Funktion nimmt
//numerische Werte skalar oder
// Matrizen
b=m_einh(4)
b=m_einh(a~) // ein skalarer Wert oder eine
// Matrixdimension
c=m_collectsp(a,1..4,7..8)
// einer oder mehrere Bereiche

Zuweisungsoperator

Zuweisungsoperator ist das Gleichheitszeichen:

a=m_null(4,4)

Konstanten

Ein paar Basiskonstanten sind implementiert

#pi // die Kreiszahl Pi
#e // die Eulersche Konstante, Basis des natürlichen Log
#true #t #w //logischen Wahr
#false #f //logisches Falsch

Zahlen

Zahlen wie in jeder Programmiersprache. Zur Zeit werden alle Zahlen noch intern im Reellen Format (extended) gespeichert; evtl. wird ein extra Ganzzahl-Modul noch eingebaut. Wo Zahlen für Indizes oder Dimensionen etc verwendet werden, wird ein evtl vorhandener Nachkommateil abgeschnitten.

123 // Integerzahl
-123 // negativ
0.345 // relle Zahl, Null ist notwendig
123.456 // relle Zahl
123.456E42 // relle zahl mal 10 hoch 42
0.123e-14 // relle Zahl mal 10 hoch -14

unäre Operatoren

Während Operationen wie a+b oder a*b als binär bezeichnet werden, (weil zwei Operanden beteiligt sind) bezeichnet man mit "unär" Operationen auf nur einem Operanden. Z.B. sind die Vorzeichen vor Zahlen (oder Variablenbezügen) unäre Operatoren, da sie sich nur auf den nachstehenden Operanden beziehen

a = -12 // unäres Minus
b = -a // wie vor
c = a * -b // vor dem Malnehmen wir b negiert
x = c^-3 // vor dem Potenzieren wird negiert

f = NOT w // Negation (wenn w boolesch ist)

a = 5 ! // fakultätsfunktion
a = 4.5 ! // wie a=gamma(5.5)

a = sqrt(b#) // matrix b als array behandeln:
// wurzeln aus elementen ziehen,
// nicht die Matrixwurzel
a = m_null(b~) // Nullmatrix mit gleicher Dimen-
// sion wie b erstellen

binäre Operatoren

Hier sind die üblichen Rechenoperatoren vorhanden, sowie eine Zahl an Operatoren für Logik, Matrizen und Strings. Als Operand kann statt einer Konstanten (Zahl etc) oder Variable (Skalar, Matrix) auch wiederum ein Ausdruck stehen, der sinnvollerweise geklammert wird, wenn die implizite arithmetische Prioritätenregelung nicht ausreicht.

c = a + b // addition
c = a - b // subtraktion

c = a * b // Multiplikation,
// Matrizen: Matrixmultiplikation
c = a * b# // matrix b wird als Array gefaßt
// à Elementweise Multiplikation
c = a / b // subtraktion
// Matrizen: a * M_INV(B) mit
// c*b = a
c = a / b# // matrix b wird als Array gefaßt
// à Elementweise Division

c = a ^ b // Potenzierung
// b darf z.Zt nur skalar sein
c = a# ^ b // matrix a wird als Array gefaßt
// à Elementweise Potenzierung

c = a div b // Ganzzahldivision
c = a mod b // Rest einer Ganzzahlsdivision
c = a over b // (a+b)!/(a!*b!)
c = a ovrmod b // (a over b) mod b

c = a & b // logisches UND
c = a | b // logisches ODER
c = a NAND b // logisches Nicht-UND
c = a NOR b // logisches Nicht-Oder
c = a XOR b // logisches exklusives oder

c = a || b // Matrix,Strings:
// Horizontale verkettung
c = a ++ b // "Matrixaddition", s.u.

allgemeine Funktionen

Diese Funktionen kann man auf Skalare ebenso wie auf Matrizen anwenden. (Soll bei Matrizen die Funktion auf die Einzelelemente angewendet werden, muß die Matrix mit dem #-Arrayoperator in einen Array umgewandelt werden).

Typen: G:skalar oder Matrix,
B:skalare boolean,
I:skalarer Integer
R: skalare reelle Zahl

· allgemeine Funktionen

;Bei Matrizen: Funktion auf Einzelelemente anwenden:
;z.B.: c = funktion(G#) // Array-Operator # verwenden

c = summe(G,...) // Summe der Argumente
c = produkt(G,...) // Produkt der Argumente

c = abs(G) // Absolutwert des Arguments
c = neg(G) // negativwert des Arguments

c = sqr(G) // Quadrierung
c = sqrt(G) // Quadratwurzel

· Funktionen\Ganzzahl

c = int(G) // Ganzzahlanteil des Arguments
c = frac(G) // Dezimalanteil des Arguments

· //Funktionen\Trigonometrie (bei Matrizen durch Taylorserie berechnet).

c = ln(G) // natürlicher Logarithmus
c = exp(G) // natürliche Exponentiation

c = sinh(G) // hyperbolischer Sinus eines Bogenmaßes
c = cosh(G) // hyperbolischer Cosinus eines Bogenmaßes

c = sin(G) // Sinus eines Bogenmaßes
c = cos(G) // Cosinus eines Bogenmaßes
c = tan(G) // Tangens eines Bogenmaßes
c = arcsin(G) // Bogenlänge eines Sinus
c = arccos(G) // Bogenlänge eines Cosinus
c = arctan(G) // Bogenlänge eines Tangens

Statt eines Matrizennamens oder einer Zahlkonstanten kann natürlich auch ein kompletter Ausdruck stehen, insbesondere können die Funktionen auch geschachtelt auftreten.

c = exp ( ln(a+b)+1)

skalare Funktionen

Diese Funktionen können nur auf Skalare angewendet werden

c = not(B) // boolsche Negation auch für
// Integer-Zahlen

c = Fak(R) // Fakultät-Funktion / Gamma-Funktion

c = PrimNr(I) // die i.te Primzahl (PrimNr(1)=2),i<6345

Matrixfunktionen

; Funktionen\Matrix\Erzeugen

; Matrizen aus konstanten Werten erzeugen

c = {wert, wert...}
// 1-zeilige Matrix erzeugen
c = { {wert,wert...},mat,mat ...}
// mehrzeilige Matrix erzeugen

c = M_Mk(iZei,iSpa,r,...)
// Matrix erzeugen (zeilen,spalten,werte...
c = M_MkSp(r [,M [,...)
// Einspaltige Matrix erzeugen (werte,matrizen,...)
c = M_MkZl(r [,M [,...)
// Einzeilige Matrix erzeugen (werte,matrizen...)
c = M_MkCorr(r,...)
// symmetrische M aus oberes Dreieck,sequentiell
c = M_MkDiag(r [,M[,...)
// Diagonalmatrix aus Vektor erzeugen (werte,matrizen...)

; Matrizen mit bestimmten Strukturen erzeugen

c = M_null(Izl,Ispa)
// Erzeugt Null-Matrix
c = M_einh(Idim)
// Erzeugt Einheitsmatrix
c = M_fill(Izl,Ispa,Rwert)
// Erzeugt Matrix mit einem bestimmten Wert
c = M_Seq(rAnf,rEnd [,Istep])
// Erzeugt Matrix mit einer Sequenz von Werten

c = M_Comb(iSpa,iUG,iOG)
// Erzeugt eine kombinatorische Matrix
// (spalten, basis=OG-UG ->Basis^Spalten)

c = M_RandomN(iZei,iSpa,rMean,rStddev)
// Matrix mit normalverteilten Zufallszahlen, zeilenweise
c = M_RandomU(iZei,iSpa [,rUG,rOG])
// Matrix mit uniform verteilten Zufallszahlen,
// zeilenweise

; Matrizen einlesen aus Dateien

c = M_readHFS(Sdateiname)
// Matrix aus einer Faktoranalyse-Datei(INSIDE-R) einlesen
c = M_readCSV(Sdateiname)
// Matrix aus einer Comma-delimited-Datei einlesen
c = M_ReadHEX(Sdateiname)
// Matrix aus einer Hex-Binärdatei einlesen
c = M_ReadBIN(Sdateiname,iAnz)
// Matrix aus einer Binärdatei einlesen,
// iAnz=Anzahl der Spalten

; Funktionen\Matrix\Allg

· ; Ergebnis skalare Zahlenwerte:

c = M_Zeilen(M) // Zeilenzahl einer Matrix
c = M_Spalten(M) // Spaltenzahl einer Matrix

c = M_Max(M) // Größter Wert in Matrix
c = M_Min(M) // Kleinster Wert in Matrix

· ; Ergebnis: Matrizen

c = M_Transp(M) // Transponierte
c = M_Ar(M) // Verwenden einer Matrix als Array

; Funktionen\Matrix\Submatrizen

c = M_Reshape(M,Izl,Isp)
// Zeilen und Spalten neu dimensionieren
c = M_Rollv(M,Icount)
// Matrixzeilen vertikal rollen

c = M_Subsp(M,ISpA,IspE) // Spalten extrahieren
c = M_Subzl(M,IspA,IspE) // Zeilen extrahieren

c = M_CollectSp(M,IspA..ISpE,...)
// Mehrere Matrixspalten(-bereiche)
// extrahieren und verknüpfen
c = M_CollectZl(M,IzlA..IzlE,...)
// Mehrere Matrixzeilen(-bereiche)
// extrahieren und verknüpfen
c = M_Minor(M,Izl,Isp) // Minor extrahieren

c = M_Diag(MQ) // Diagonale extrahieren
// und als 1-sp Vektor ausgeben
c = M_DiagCopy(MQ) // Diagonale in Matrix gleicher
// Größe kopieren

; Funktionen\mehrere Matrizen

c = M_Addsp(M,) // Matrix mit Spalten zusammenfügen
c = M_Addzl(M,) // Matrix mit Zeilen zusammenfügen
c = M_Concatsp(M,) //
c = M_Concatzl(M,) //

c = M_MergeDiag(M1,M2) // Diagonale aus M2 in M1 einfügen

c = M_SeqMult(M1,M2)
// gewichtetes Addieren benachbarter
//Elemente einer Matrix (M2:Gewichtsmatrix)

; Funktionen\Matrix\Zeilen/Spalten verrechnen

· Ergebnis sind Spalten/Zeilen-Vektoren mit einer Auswertung über die Zeilen/Spalten/komplett einer Matrix

// Summen berechnen
c = M_SumZl(M) // für jede Zeile
c = M_SumSp(M) // für jede Spalte
c = M_Sum(M) // Summe aller Elemente

// Mittelwerte...
c = M_MeanZl(M) // für jede Zeile
c = M_Meansp(M) // für jede Spalte
c = M_Mean(M) // für ganze Matrix

//summe der Quadrate
c = M_SqsumZl(M) // für jede Zeile
c = M_Sqsumsp(M) // für jede Spalte
c = M_Sqsum(M) // für ganze Matrix

//Standardabweichungen...
c = M_StddevZl(M) // für jede Zeile
c = M_StddevSp(M) // für jede Spalte
c = M_Stddev(M) // für ganze Matrix

· Ergebnis sind Matrizen gleicher Größe mit ersetzten Werten

//Abweichungen vom Mittelwert (Mittelwert wird 0)
c = M_AbwZl(M) // für jede Zeile
c = M_AbwSp(M) // für jede Spalte
c = M_Abw(M) // für ganze Matrix

//Z-Werte (Standardabweichung wird 1)
c = M_zvaluezl(M) // für jede Zeile
c = M_zvaluesp(M) // für jede Spalte
c = M_zvalue(M) // für ganze Matrix

//Normwerte (Quadratsumme wird 1)
c = M_normZl(M) // für jede Zeile
c = M_normSp(M) // für jede Spalte
c = M_norm(M) // für ganze Matrix

// Zeilen de-korrelieren
c = M_UnkorrZl(M) // Zeilen de-korrelieren

; Funktionen\Matrix\Quadratisch

c = M_Inv(MQ) // Inverse einer quadr. Matrix

c = M_Det(MQ) // Determinante einer quadr. Matrix
c = M_Spur(MQ) // Spur einer quadr. Matrix

; Funktionen\Matrix\Distanz

c = M_Dist(M1 [,M2'][,iNorm])
// Matrix der (Zeilen-)Distanzen
// (zu Norm deflt 2)

; Funktionen\Matrix\Kovarianz

; Funktionen\Matrix\Kovarianz\Faktorisieren

c = M_GS(MCOV) // Cholesky-Zerlegung
c = M_Cholesky(MCOV) // Cholesky-Zerlegung
c = M_Decompose(MCOV) // Vollständige Dekomposition
c = SQRT(MCOV) // auch hiermit kann man
// faktorisieren

; Funktionen\Matrix\Kovarianz\Kommunalitätenschätzung

c = M_GetIndiv(MCOV) // 1-Multiple-r² für jede Variable bestimmen
c = M_ComVar(MCOV) // Common Varianz per dyn. Approx.
c = M_ComVarPCA(MCOV) // Common Varianz per PCA Approx.
c = M_ComVarFix(MCOV) // Common Varianz per fix. Approx.
c = M_ComVarPaf(MCOV,IFanz) // Common Varianz per PAF
// Approx.;ANzahl der Faktoren

; Funktionen\Matrix\Kovarianz\Rotationen

; c = M_Rot(LAD,Srottyp)
// Spaltenrotationen einer Matrix
// (S=Typauswahl)
c = M_Rot(LAD,"Tri")
c = M_Rot(LAD,"PCA")
c = M_Rot(LAD,"Quartimax")
c = M_Rot(LAD,"Medimax")

; Funktionen\Matrix\Kovarianz\Sonstiges

c = M_CovToCorr(MCOV)
// Kovarianz in Korrelation umwandeln
c = M_RemVar(MCOV,<ivarnr>)
// Faktor 1-er Variabler extrahieren

; Funktionen\Matrix\R2/R3-Funktionen

;Raum-2 wie Komplex (a,b)=a+bi


c = R2_Add(V2) // R2-Addition
c = R2_Sub(V2) // R2-Subtraktion
c = R2_Mul(V2) // R2-Multiplikation
c = R2_Div(V2) // R2-Division
c = R2_ToR3(V2) // R2 nach R3 Umwandlung

;Raum-3 (a,b,c)= a+b*p+c*q (p,q komplexe 3.Wurzeln aus 1)

c = R3_Add(V3) // R3-Addition
c = R3_Sub(V3) // R3-Subtraktion
c = R3_Mul(V3) // R3-Multiplikation
c = R3_Div(V3) // R3-Division
c = R3_ToR2(V3) // R3 nach R2 Umwandlung
c = R3_Norm(V3) // R3 normieren

Referenzen

SPSS^®-Formatbeschreibungen

von SPSS ausgeben (SPSS-Steuerbefehle):

· CSV-Format

SAVE TRANSLATE
OUTFILE='FZA_FAC3.csv'
/TYPE=TAB
/KEEP S1a188 to s1a207 fak1 fak2 fak3
.

· HEX-Format (für MatMate empfohlen)

write cases
outfile ='f:\temp\simplex\bihex.txt'
records=1
/1 f1 to f6 (6rbhex8).

· BIN-Format

write cases
outfile="f:\temp\decomp8_SPSS^®1.bin"
records=1
/1 f1 to f6 (6rb8) .

nach SPSS einlesen (SPSS-Steuerbefehle):

· BIN-Format

file handle dat2 name="f:\temp\decomp8.bin"
/recform=fixed
/lrecl=50
/mode=image.

data list file=dat2
/1 f1 to f6 (6rb8) nl (a2).

execute.

· HEX-Format (für MatMate empfohlen)

data list
file ='f:\temp\simplex\bihex.txt'
records=1
/1 f1 to f6 (6rbhex8).

Einlesen aus Inside-[R]

HFS-Files der Inside-[R]-Versionen bis 3.6 können direkt in MatMate eingelesen oder aus MatMate ausgegeben werden.

inside-r mymatrix

ist jetzt eine direkte Schnittstelle in MatMate.

Programmierumgebung für MatMate:

Borland-Pascal Delphi Version 6. Entwicklerhandbuch

Copyrights und Markennamen

· SPSS^® ist Markenzeichen der SPSS^® Inc., USA, Chicago

· Delphi^® ist Markenzeichen von Borland Corp. USA

· Windows^® ist Markenzeichen von Microsoft Corp, USA

· Das Programm MatMate ist nicht für kommerzielle Nutzung, sondern nur für Anwendung in Ausbildung und Selbststudium freigegeben. Sie können sich die aktuelle Test-Version für Evaluationszwecke downladen. Weitergabe und Referenz nur mit Angabe des Programmautors/email-Adresse. Rückmeldungen über Fehler oder Erweiterungsoptionen an den Autor erwünscht.