Wie gut sind die Voraussagen?
Das lineare Regressionsmodell
Wir betrachten wieder unser Beispiel...
Durch die Vorhersagewerte weiß Hermine nun, wie viel Wasser sie je nach voraussichtlicher Streckenlänge mitnehmen muss. Sie weiß jedoch auch, dass sie im Sommer mehr trinkt als etwa im Herbst, und dass sie im Allgemeinen an manchen Tagen mehr trinkt als an anderen.
Wie verlässlich ist nun also die Schätzung der Wassermenge, die sie durch das lineare Regressionsmodell erhalten hat?
Der Determinationskoeffizient R2
Der Determinationskoeffizient R2 wird auch als Bestimmtheitsmaß oder Varianzaufklärung bezeichnet. Er gibt an, welcher Anteil der Varianz der abhängigen Variable durch die (jeweilige) unabhängige Variable erklärt wird.R2 ermittelt sich dabei aus der erklärten Varianz der abhängigen Variable geteilt durch die gesamte Varianz der aV:
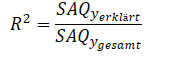
Und bewegt sich dabei im Wertebereich zwischen 0 und 1:
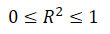
Durch die Ermittlung von R2 erhalten wir also einen Anteilswert, der mit 100 multipliziert den Prozentwert darstellt, welcher angibt, wie viel der Gesamtvarianz durch die unabhängigen Variable(n) erklärt werden kann. D.h. je höher R2, desto verlässlicher sind die Schätzungen anhand der Regressionsgleichung und desto höher ist die Modellgüte.
Liegt R2 also hoch, kann Hermine davon ausgehen, dass sie mit ihrem Regressionsmodell die benötigte Wassermenge verlässlich voraussagen kann. Liegt es besonders niedrig, kann sie keine sonderlich verlässlichen Vorhersagewerte ermitteln.
PRE-Logik
Der Determinationskoeffizient R2 ist ein sogenanntes PRE-Logik Maß (Proportional Reduction of Errors). Bei PRE-Logik Maßen erfolgt die beste Schätzung auf Basis der Verteilung.D. h. bei R2 reduzieren wir mögliche Prognosefehler dadurch, dass die Vorhersage der y-Werte mit Kenntnis der Werte der unabhängigen Variablen erfolgt. So erhalten wir eine bessere Schätzung als bei einer Vorhersage der y-Werte ohne Kenntnis der Werte der unabhängigen Variablen.
Der korrigierte Determinationskoeffizient R2korr
Von statistischen Modellen wird gefordert, dass sie eine hohe Erklärungskraft, zugleich jedoch eine geringe Komplexität besitzen.Tatsächlich wächst mit der Anzahl der erklärenden Variablen (uVs) nicht nur die Erklärungskraft, sondern ebenso die Komplexität des Modells. Dadurch lassen sich die Determinationskoeffizienten von linearen Regressionsmodellen mit verschiedener Anzahl an erklärenden Variablen nicht miteinander vergleichen.
Um dieses Dilemma zu lösen, gibt es den korrigierten Determinationskoeffizienten R2, der sich folgendermaßen berechnet:
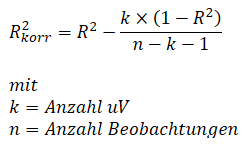
Bereinigt um den Einfluss der Anzahl der unabhängigen Variablen, lassen sich die korrigierten Determinationskoeffizienten und somit die Qualität der Prognosen nun miteinander vergleichen.