Übersicht statistischer Tests
Prüfgröße  Teststatistik  Was wird getestet? Ermittlung kritischer Wert Aussehen der Verteilung
Anteilswert z-Wert Kann der in der SP gefundene Anteil auf die GG verallgemeinert werden? z-Tabelle (α abhängig von Richtung des Tests)
χ2 (Chi-Quadrat) χ2 Ist der Zusammenhang zwischen zwei kategorialen Variablen auf die GG verallgemeinerbar? Fester kritischer Wert:
χ2krit = 3,841
Korrelationskoeffizient t-Wert Gilt der Zusammenhang zweier metrischer Variablen auch in der GG? t-Tabelle (auf Anzahl der Freiheitsgrade (df) achten!)
F-Wert (Effekte der Gruppenzugehörigkeit) F-Wert Ist der Zusammenhang zwischen Gruppenzugehörigkeit (kategoriale uV) und der metrischen aV auch in der GG gültig? F-Tabelle (ablesen als df = v1, v2 mit v1=Freiheitsgrade des Zählers & v2=Freiheitsgrade des Nenners)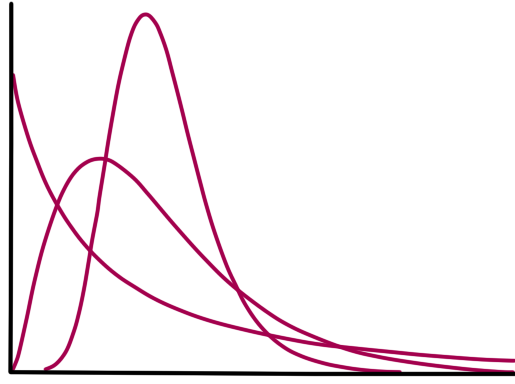
Der Hypothesentest über einen Anteilswert ist nur einer von vielen statistischen Tests.
Die Tests unterscheiden sich zwar in Prüfgröße, Teststatistik und Funktion/Anwendungsbereich. Sie folgen jedoch aller der vorgestellten Logik.
In der Tabelle sind noch einmal die für Sie für die Statistik 1 Vorlesung wichtigen Hypothesentests zusammengefasst.
Die Normalverteilung ist eingipflig, symmetrisch und nähert sich der x-Achse auf beiden Seiten asymptotisch an. Maximum des Graphen ist der Erwartungswert μ und die Wendepunkte liegen bei μ-σ und μ+σ. Die Fläche unter dem Graphen beträgt 1; der Bereich zwischen den Wendepunkten deckt bereits 68% der Fläche ab. Wegen seines Aussehens wird der Graph auch als Gaußsche Glockenkurve bezeichnet.
Das Aussehen der Chi-Quadrat-Verteilung ist abhängig von der Anzahl des sogenannten Freiheitsgrades (df). Das Maximum des Graphen liegt bei df-2 für alle df≥2. Der Erwartungswert μ entspricht dem jeweiligen Freiheitsgrad. Die Chi-Quadrat-Verteilung ist linkssteil bzw. rechtsschief, d. h. Werte, die kleiner als μ sind, sind häufiger zu beobachten. Je größer die Anzahl der Freiheitsgrade ist, desto weniger schief ist die Verteilung, wie in der Grafik zu sehen ist. Die Kurve ganz rechts besitzt die meisten Freiheitsgrade und die Schiefe ist kaum noch erkennbar.
Die t-Verteilung ist der Normalverteilung sehr ähnlich. Sie findet ihre Anwendung, wenn die Standardabweichung σ der Grundgesamtheit unbekannt ist. Auch sie ist eingipflig, symmetrisch und nähert sich der x-Achse auf beiden Seiten asymptotisch an. Die Fläche unter der Kurve beträgt ebenfalls 1. Sie ist jedoch endlastiger als die Normalverteilung, d. h. sie generiert eher Werte, die weit vom Mittelwert entfernt liegen. Ihr Aussehen ist ebenfalls von Freiheitsgraden abhängig. Zudem gibt es noch die nichtzentrale t-Verteilung.
Bei der F-Verteilung handelt es sich um die Wahrscheinlichkeitsverteilung einer metrischen Variablen. Sie wird verwendet, um zu überprüfen, ob die Grundgesamtheiten zweier Stichproben die gleiche Varianz besitzen. Die F-Verteilung besitzt zwei Parameter, bei denen es sich um die unabhängigen Freiheitsgrade v1 & v2 handelt (Schreibweise: df = v1, v2).
Klicken Sie auf die farblich hinterlegten Teststatistiken für die Formeln!
Klicken Sie auf die Graphen der Verteilungen, um sie sich genauer anzusehen!