Project 11
P11: Model reduction via symmetries and conservation laws for systems on multiple time scales
Project description
Most mathematical models of biological clocks consist of parametric systems of differential or difference equations. As the models often consist of dozens or even hundreds of equations and many more parameters (many of which are usually redundant), it is almost impossible to perform a rigorous mathematical analysis of them. In the literature, one can find many different model reduction techniques. Most of them are, however, of a numerical nature and easily destroy more complex features like oscillations, in particular if these combine modes on different time scales. We will instead focus on exact reduction methods which automatically preserve all qualitative features of the model. Key tools will be symmetries and conservation laws and their extension and adaption to systems with multiple time scales.
Conservation laws almost always provide important insights. Unfortunately, it is not easy to find them. In particular, for biological systems typically only linear conservation laws are known, as these can be constructed in a simple manner. We are currently applying machine learning for the discovery of nonlinear conservation laws of dynamical systems. Opposed to all approaches in the literature, we are not using neural networks but kernel methods, as these require much less data and computing time. This is particularly relevant, if not synthetic numerical data are used but experimental data which cannot easily be produced in arbitrarily large quantities.
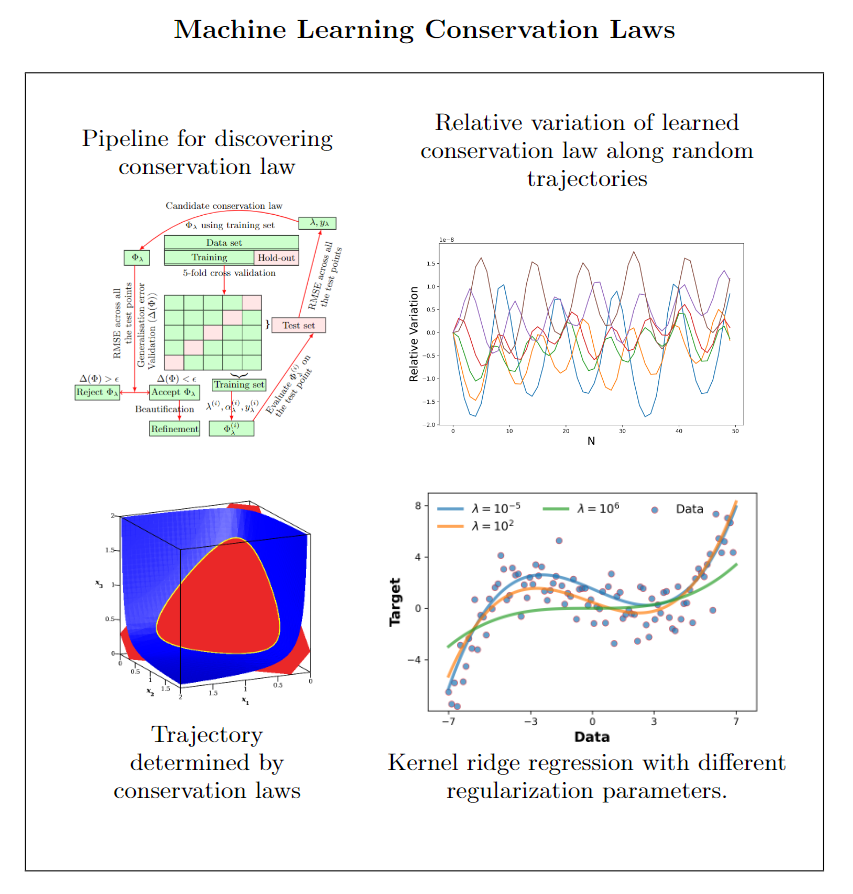
Estimation of parameters in mathematical models from experimental data requires that the parameters are structurally identifiable. For many years, it has already been known that symmetry methods allow for deciding whether or not in a dynamical system parameters possess this property. We are particularly interested in distinguishing between globally and only locally identifiable parameters and conjecture that the latter ones are related to the existence of discrete symmetries and not the better known Lie symmetries. We are currently developing methods (and computer programmes) for deciding whether or not a dynamical system admits such symmetries.
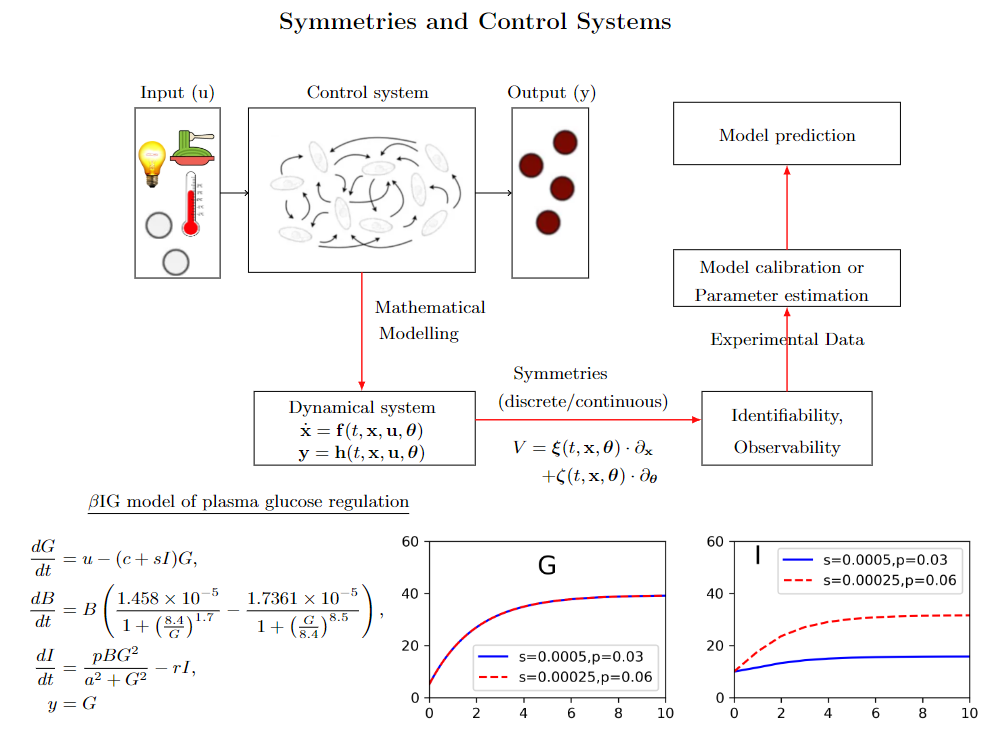
In both directions, a major question for the future is the extension of our results to approximate conservation laws and symmetries. Opposed to physical models which are often built upon symmetry principles and thus naturally possess many exact conservation laws, biological models are of a phenomenological nature and thus inherently of an approximate nature. We therefore expect that they possess only very few exact conservation laws. But it might happen much more frequently that some quantities are approximately conserved, i.e. their changes can be noticed only after some lengthy period of time or the changes almost disappear after a transient phase. Similarly, a dynamical system on multiple time scales may not possess exact symmetries (discrete or continuous), but approximate symmetries on certain time scales.
Publications
M. Abebaw Mebratie, R. Nather, G.F. von Rudorff, W.M. Seiler: Machine Learning Conservation Laws of Dynamical Systems. Preprint; arXiv:2405.20857 (2024). https://arxiv.org/abs/2405.20857
